Solving the Point-in-Polygon Calculation Challenge: Tips From Top Engineers

The ‘point in polygon’ problem is a common challenge in geospatial analysis that involves determining whether a given 2D point (denoted by lat/long) is located within a polygon or not. This problem frequently arises in various use cases, such as reverse geocoding, geo-smart routing and fleet management systems.

The problem can be solved using various algorithms and techniques, including ray casting.

The ray casting algorithm, also known as the crossing number algorithm, dates back to 1962 and continues to be widely used today.

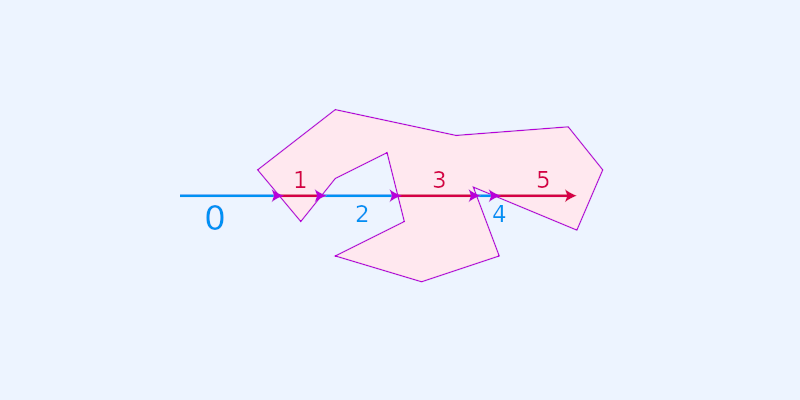
While some may argue that the algorithm has limited precision for coordinates near the polygon boundary and other factors, it is generally considered suitable for geospatial applications.

The challenge with ray casting algorithm

The real problem with this approach is that it has linear time complexity and handles complex polygons quite slowly. To give some general figures, one could expect to spend a couple of hundred milliseconds or even seconds on complex polygons. If this is a step of an online API, it could significantly impact the P50 and P95 latencies.

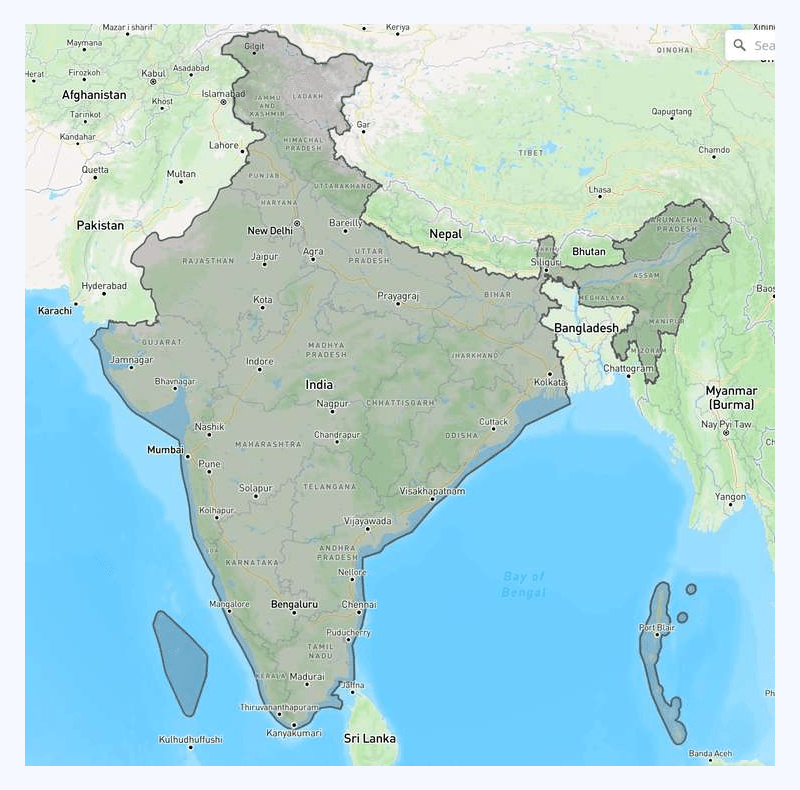
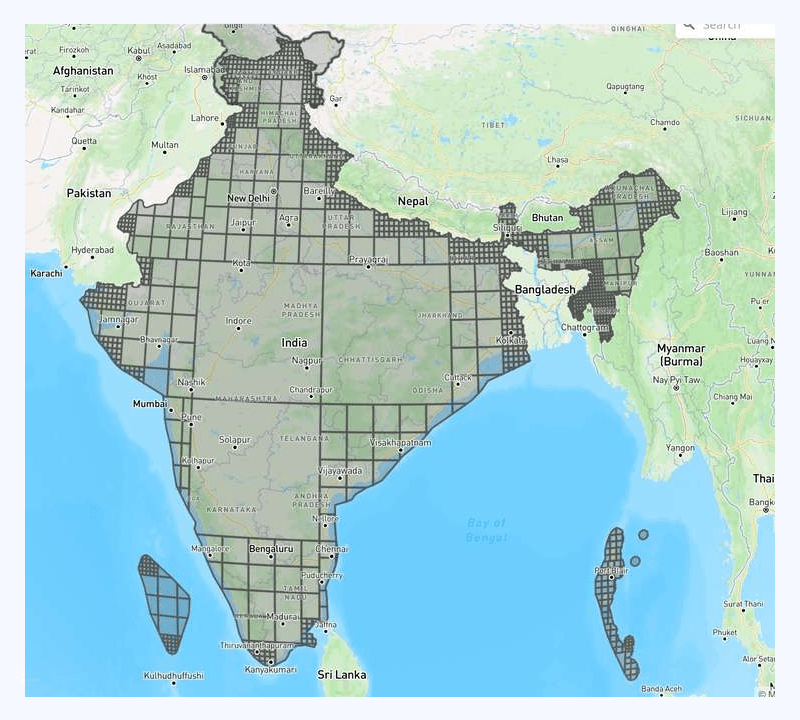
Complex polygons are not strangers to geospatial systems. Let’s look at one real-life example:

Now, this is a fairly complex polygon. If we zoom in a bit, there are more coordinates in the contour than what one might get as an impression from the screenshot. It is expensive in terms of latency to tell whether a random geolocation is within the polygon.

Of course, simple optimizations can be done here. We can calculate the bounding box and use it to rule out geolocations not even within the bounding box first. This approach helps, but more is needed as a whole solution.

In software engineering, we always try to split huge problems into smaller ones that we have more confidence in solving.

In this specific case, it is hard to calculate point-in-polygon efficiently for such a complex polygon. But can we divide the complex polygon into multiple not-so-complex ones and do the calculation then?

The answer is YES.

Simplifying the complex point-in-polygon calculation

If we split the big/complex polygon into smaller/less-complex ones, we could put them into a geospatial index like R-tree and calculate point-in-polygon much more efficiently. The potential matching candidates can be located in LgN (logarithmic time), and the system can determine whether the candidate is a real match in constant time. This is, of course, when we expect that the split polygons are simple enough for point-in-polygon calculations to be performed quickly.

A similar mathematical problem is called polygon triangulation. What it does is that it tries to split complex polygons into smaller triangles, and we know triangles are efficient in point-in-polygon calculations since they only have three vertices. This works great in gaming and computer graphics in general but not as well in geospatial use cases. The reason is that split triangles have many overlapping bounding boxes, making R-tree locating matching candidates less efficient.

Attempt 1

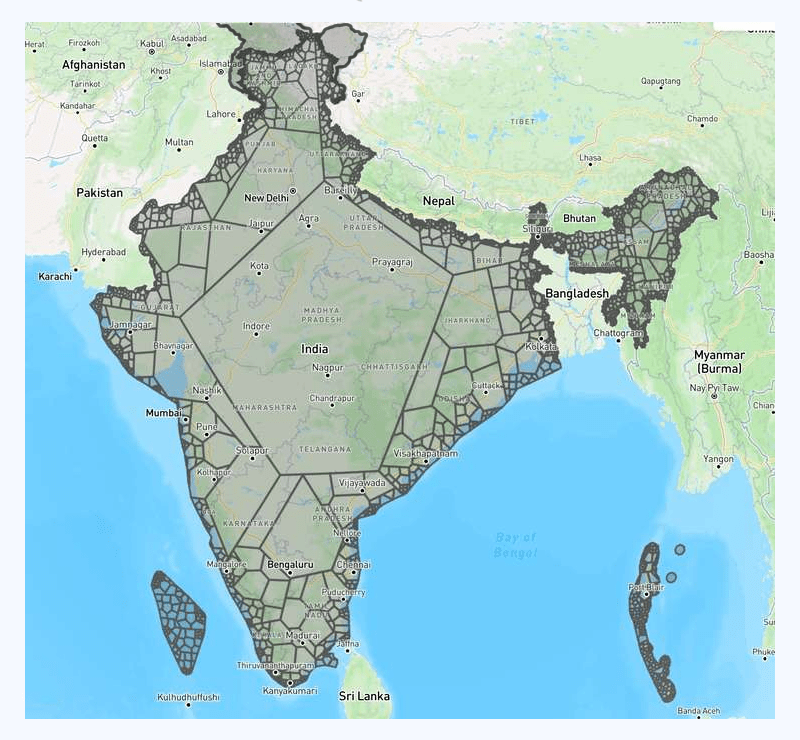
There are also other mathematical ways to partition a polygon, such as partitioning a polygon into trapezoids. There are many existing implementations around, and we tried to follow one of them, which gives the following result:

In the image above, you can easily tell we split the raw polygon recursively here.

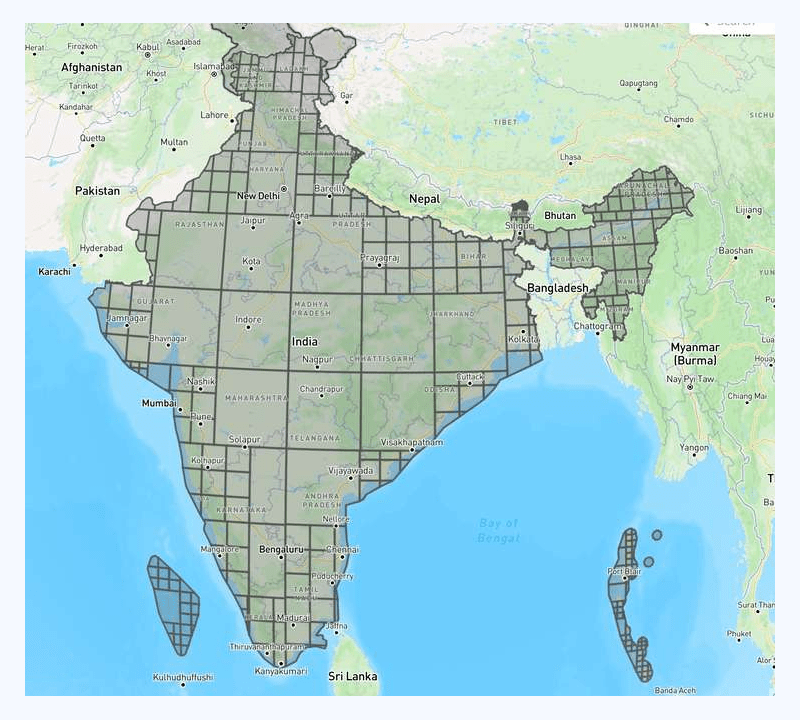
Attempt 2

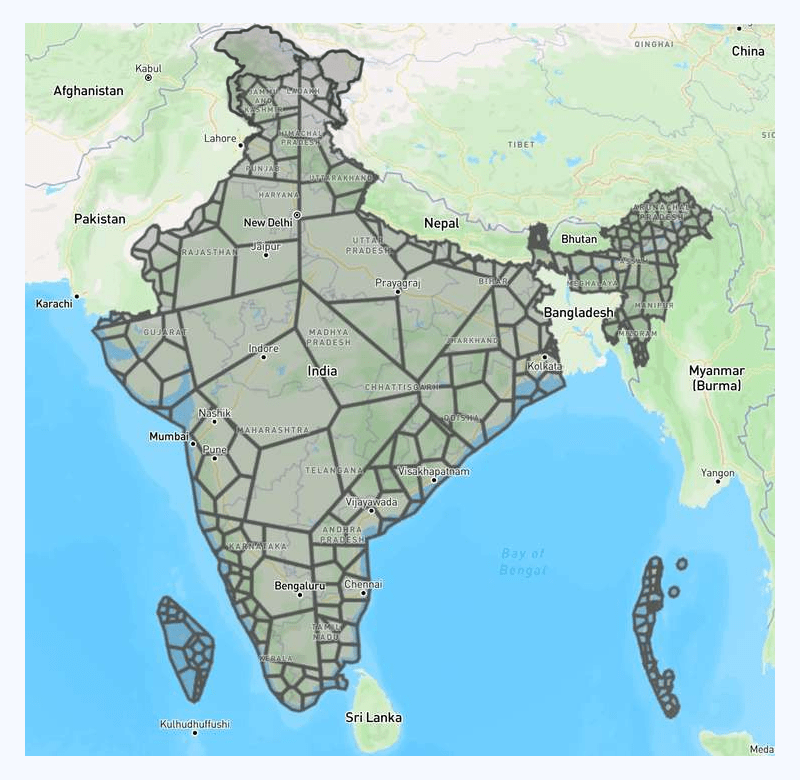
With some tuning on recursive parameters, we got the following result:

The above result is definitely better. The end performance (point-in-polygon calculation efficiency) improved by 80x compared to raw point-in-polygon calculation.

Although a better alternative than the triangulation method, this approach still results in significant overlap of R-tree elements.

Attempt 3

We stopped implementing mathematical equations because we realized that what works best for computer graphics might not work super well in geospatial use cases. We know that R-tree loves rectangles because that is the index they are using internally, then why did we try to fight with it instead of going along with it? With these thoughts, we implemented another recursive splitting from scratch, which gives the following result:

We found that the number of small boxes did not meet our requirements, prompting us to carry out additional tuning measures to optimize the system.

The final result

This time, we got the following results:

We know that this design looks impressive and would perform exceptionally. The end test shows that our point-in-polygon calculation efficiency improved by 100x!

Key insights and takeaways

After testing out various approaches to solving the point-in-polygon calculation challenge, several key findings and insights emerged. Specifically, we found that:

1. It is inefficient to store and calculate point-in-complex polygons as is.
2. We can pre-process and split the complex polygon into a list of smaller ones and load them into R-tree.
3. We could achieve more runtime efficiency with more memory/storage consumption.

Careful tuning of algorithm parameters can further enhance performance and accuracy. These insights provide valuable guidance for engineers seeking to optimize point-in-polygon calculations in their applications.