Table of Contents
When it comes to logistics and transportation, being efficient is key to success. A huge number of vehicles use complicated networks of roads every day to deliver goods and services to customers all over the world. But it’s very hard to find the best ways to use these routes so that they use resources efficiently, cost as little as possible, and still meet strict delivery requirements. The Capacitated Vehicle Routing Problem (CVRP) becomes an important puzzle to solve at this point.
How to Understand CVRP
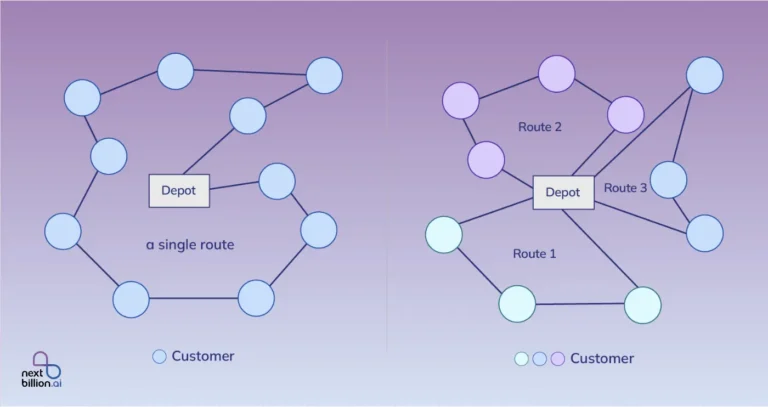
At its core, CVRP is about figuring out the best routes for a fleet of vehicles to take to deliver goods to a group of customers while still meeting the limits of each vehicle’s capacity. The problem is made even more difficult by the fact that there is a central depot where all the vehicles leave from and return to after making deliveries. Every customer has different needs, and vehicles have to stay within their weight limits so that all deliveries can happen.
Complexity and Use in the Real World:
CVRP is a classic sequential optimization problem that is used in many fields, including public transportation, e-commerce, retail, and trash collection. Because it gets exponentially harder to compute as the number of customers grows, it is called NP-hard. Even though it is hard to understand on a theoretical level, CVRP is very important in real life because it is an important part of supply chain management and logistics operations.
How to exactly solve the problem of capacitated vehicle routing
Finding the best routes for a fleet of vehicles to serve a group of customers while staying within the limits of each vehicle’s capacity is what CVRP is all about. Heuristic and metaheuristic methods give you close answers, but exact methods promise the best answers by looking through the whole solution space.
Branch and Bound
Branch and Bound is an algorithmic method that is often used to solve CVRP and other combinatorial optimization problems. By branching on decisions and limiting the search to get rid of less-than-ideal solutions, the method systematically explores the solution space.
How it works:
Branching: The solution space is broken up into smaller problems, or branches, that are easier to handle.
Bounding: A lower bound is found on the objective function for each subproblem. The subproblem is thrown away if this bound is higher than the best-known solution.
Pruning: Parts of the search tree that can’t lead to better solutions are cut out.
Advantages:
Guarantees the best solution.
Pruning can greatly reduce the search space if done right.
Disadvantages:
Can be hard on computers when there are a lot of them.
For it to be useful, it needs effective bounding and branching strategies.
Branch and Cut
Adding cutting planes to Branch and Cut makes the linear programming relaxation of the problem tighter. Branch and Cut is an extension of Branch and Bound.
How it works:
Branching is like Branch and Bound.
Cutting: To get rid of fractional solutions, more constraints (cuts) are added to the linear relaxation. This makes the feasible region smaller.
Cutting Down: Just like in Branch and Bound, cutting down and adding to the search space is done with bounding and pruning.
Advantages:
Often works better than Branch and Bound by itself.
Using cutting planes, it is possible to solve larger cases to their best solution.
Disadvantages:
Because of the need for effective cuts, implementation is hard.
The extra work that needs to be done to add cuts.
Dynamic programming
Dynamic programming (DP) splits the CVRP into smaller problems that can be solved more quickly. The solutions to each smaller problem are saved so they can be used again later.
How it works:
Define the state by looking at the partial routes and the amount of capacity that is still available.
Recursive Solution: Work your way up to solving the main problem by solving subproblems one at a time.
Memorization: Save the answers to subproblems so that you don’t have to do the same calculations twice.
Advantages:
Can give exact answers to problems of a moderate size.
takes advantage of subproblems that overlap and optimal substructure.
Disadvantages:
The number of customers makes the state space grow very quickly.
Not useful for large instances because of memory and processing limits.
Integer Linear Programming (ILP).
ILP formulations show CVRP as a set of linear equations and inequalities with integer variables.
How it works:
Formulation: Write down the problem in the form of a decision matrix, an objective function, and some constraints.
Solving: To find the best answer, use an ILP solver (such as CPLEX or Gurobi).
Advantages:
Utilizes strong business solvers.
The ability to model different constraints and goals.
Disadvantages:
It may take a long time to compute.
For big problems, it needs good formulations and fast solvers.
How to solve the Capacitated Vehicle Routing Problem (CVRP) using heuristics and metaheuristics
Logistics and transportation are fields that are always changing. One of the most important challenges is finding the best routes for a fleet of vehicles to deliver goods as quickly as possible. In the Capacitated Vehicle Routing Problem (CVRP), you have to find the most efficient routes for vehicles that are limited in how many people they can carry.
Even though exact methods give the best answers, they are often not useful for big problems because they require a lot of computing power. Heuristic and metaheuristic approaches can help with this by giving us workable and almost perfect solutions in a reasonable amount of time.
Heuristic Methods
Heuristics are ways to solve problems that use useful techniques to come up with quick solutions that are good enough to handle complicated issues.
1. Google’s Nearest Neighbor Search
The Nearest Neighbor Algorithm is a simple greedy heuristic that builds a route by picking the closest customer who hasn’t been visited yet over and over again.
How it works:
Go to the depot to begin
Choose the closest unattended customer that fits the vehicle’s size.
Do this again and again until all customers have been seen or until the current vehicle can’t take any more customers.
You should go back to the depot and start a new route if there are still customers.
Advantages:
Simple and easy to use.
Offers an instant answer.
Disadvantages:
Can lead to solutions that aren’t the best.
Local optima can happen.
2. Savings Algorithm
Clarke and Wright came up with the Savings Algorithm, which is another heuristic that combines routes to try to cut down on the total distance.
How it works:
At first, use a separate route for each customer.
Find the savings from combining routes.
Combine routes that save the most money while still meeting capacity needs.
Do this again and again until you can’t merge any more routes.
Advantages:
It is more complex than the Nearest Neighbor Algorithm.
Usually leads to better solutions.
Disadvantages:
You might not find the global best yet.
Needs careful application of merging criteria.
Metaheuristics Methods
Metaheuristics are more advanced steps that help heuristics get out of local optimal conditions and better explore the solution space.
1. Genetic Algorithms
Genetic algorithms try to find solutions to optimization problems by copying the way natural selection works.
How it works:
Initialization: Come up with a first set of solutions.
Selection: Look at all the possible solutions and pick the best one.
Crossover: Put two solutions together to make a new solution.
Mutation: Change some solutions in a random way.
The selection, crossover, and mutation steps should be done again and again until convergence or a stopping criterion is met.
Advantages:
Good for exploring big areas of possible solutions.
Can get out of local optima.
Disadvantages:
needs the parameters to be carefully tuned.
Intensive in computing.
2. Annealing on a computer
The process of annealing in metalworking, which involves heating and controlled cooling, is the basis for simulated annealing.
How it works:
Start by coming up with a first solution.
Make small changes to the solution over and over again.
Change your mind based on a chance that gets smaller over time (temperature).
Cool the system down slowly to lower the chance of accepting worse solutions.
Advantages:
Simple and useful.
Can get out of local optima.
Disadvantages:
Needs the cooling schedule to be carefully tuned.
Getting closer can take a while.
3. Ant Colony Optimization (ACO)
Ant Colony Optimization is based on how ants find the best places to eat by following pheromone trails.
How it works:
Set the levels of pheromones on all routes to zero.
Play as ant agents who use pheromone strength and heuristic information to build solutions.
Change the pheromones based on how good the solutions are that were found.
Repeat until there is convergence or a stopping point is reached.
Advantages:
Works well for problems involving combinatorial optimization.
Will be able to adapt to changes.
Disadvantages:
Needs to be tuned in several ways.
It takes a lot of time to compute for big problems.
4. Tabu Search
Tabu Search is an iterative algorithm that uses memory structures to keep from going back to solutions that have already been found.
How it works:
Start by coming up with a first solution.
Move over and over to the best neighboring solution that is not tabu, which means it is not against the memory structure.
Add the most recent moves to the tabu list.
Keep going until convergence or a certain point is reached.
Advantages:
Good at staying away from local optima.
Can deal with solution spaces that are big and complicated.
Disadvantages:
Needs careful planning of the tabu list.
Intensive in computing.
Hybrid Approaches
When you mix heuristics and metaheuristics, you can get powerful hybrid approaches that find a good balance between exploring and exploiting.
1. Neighborhood search that changes
Variable Neighborhood Search changes the structures of the neighborhoods in a planned way while the search is going on so that different solutions can be tried.
Advantages:
Can get out of local optima well.
able to bend and change to fit different situations.
2. Algorithms for Memetic
Memetic algorithms improve solutions over and over again by combining genetic algorithms with local search methods.
Advantages:
Balances search on a global and local level.
Can come up with good solutions.
Optimizing vehicle routes while considering capacity constraints is a complex challenge, but NextBillion.ai’s Route Optimization API makes it manageable with its smart approach to the Capacitated Vehicle Routing Problem (CVRP). The CVRP involves planning the most efficient routes for a fleet of vehicles with limited capacities to service a set of deliveries.
Understanding Multidimensional Capacity
The key to solving the CVRP effectively lies in accurately defining the capacities of each vehicle in multiple dimensions. Vehicles often carry loads that differ in volume, weight, and item count. For example, a delivery truck might have a capacity of 10 cubic meters for volume, 1000 kg for weight, and 6 pallets for items. These capacities must be respected simultaneously to avoid overloading and ensure safe, efficient transportation.
How NextBillion.ai Handles Multidimensional Capacity
NextBillion.ai’s Route Optimization API allows businesses to define the capacities of their vehicles using a multidimensional array. This means you can specify different capacity limits for volume, weight, and item count, ensuring the optimization algorithm considers all relevant factors when assigning shipments to vehicles.
Example Scenario
Imagine a construction company with a fleet of trucks used to transport various materials, such as bricks, cement, and construction workers. Each truck has different capacities for weight, volume, and personnel:
- Weight: 100 kg
- Volume: 10 cubic meters
- Personnel: 5 construction workers
In this scenario, the capacity parameter for a truck can be defined as [100, 10, 5]. This multidimensional capacity ensures that the total load assigned to each vehicle does not exceed its limits in any dimension.
By leveraging this detailed capacity information, NextBillion.ai’s optimization algorithm can assign jobs and shipments to the appropriate vehicles, enhancing operational efficiency and customer satisfaction.
Benefits of Multidimensional Capacity Optimization
- Improved Efficiency: Ensures optimal use of vehicle space and weight capacity, reducing the number of trips needed.
- Enhanced Safety: Prevents overloading, which can lead to accidents and increased wear and tear on vehicles.
- Better Customer Service: By optimizing deliveries, businesses can ensure timely arrivals and improved service reliability.
An approach that takes the best parts of different approaches and puts them together can work very well in real life. It is possible to get good solutions quickly by first using heuristics to find solutions and then making them better with metaheuristic techniques.
NextBillion.ai’s Route Optimization API offers a robust solution for businesses facing the complexities of the Capacitated Vehicle Routing Problem. By accurately defining and managing multidimensional vehicle capacities, the API enables efficient, safe, and reliable route planning.
About Author
Rishabh Singh
Rishabh Singh is a Freelance Technical Writer at NextBillion.ai. He specializes in Programming, Data analytics and technical consulting, turning complex tech into clear and engaging content.