Table of Contents
Route Optimization Problem-Minimizing Vehicles
Introduction
In today’s fast-paced world, efficient transportation systems play a crucial role in ensuring the smooth flow of goods and services. As businesses strive to improve their operations and reduce costs, optimizing routes for vehicles has become a paramount concern. The “Route Optimization Problem: Minimizing Vehicles” technical notebook delves into the challenges and strategies associated with minimizing the number of vehicles required to fulfill a set of tasks efficiently.
The route optimization problem involves determining the most optimal paths for a fleet of vehicles to visit a given set of locations while meeting specific constraints and objectives. This problem is of great significance across various industries, including logistics, transportation, delivery services, and public transportation, where reducing the number of vehicles can lead to significant cost savings and reduced environmental impact.
In this notebook, we’ll guide you through a sequence of iterative steps to find an optimal solution that meets a customer’s requirement to minimize the number of vehicles being used in the context of the Multi-Vehicle Routing Problem (MVRP).
Objective Function
The main objective of the routing optimization problem is to minimize the total cost of transportation for all customers, considering the transportation cost for each customer from one location to another. The cost can be measured as either travel time or travel distance, and the goal is to find the optimal assignment of customers to vehicles while ensuring that each customer’s demand is met and not exceeded.
The objective function can be defined as follows:
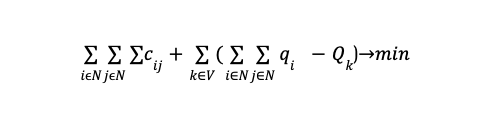
Where
- N represents the set of customers (1, 2, …, n) that need to be serviced.
- Cij denotes the transportation cost for the customer from location i to location j.
- V is the set of all available vehicles, with k∈V representing each vehicle.
- d represents the demand of the customer going from location i to location j.
- qi represents the demand or capacity required at location i.
- Qk denotes the maximum capacity of vehicle k for k∈V.
Scenario and Iterative Solutions
For this particular scenario, the goal is to start with a certain number of vehicles and run four route optimization solutions, each incrementing the number of vehicles by some value. This approach allows the planner to iteratively refine the solution and ultimately determine the optimal or minimum number of vehicles required for the given problem.
Scenario Overview
Imagine you are managing a fleet of vehicles for a logistics company, and your goal is to efficiently deliver goods to a set of customers while minimizing the number of vehicles used. The problem is known as the Multi-Vehicle Routing Problem (MVRP).
Initial Assumption
At the outset, you begin with an assumption or initial estimate of the number of vehicles required to serve all the customers effectively. This initial estimate may be based on historical data, intuition, or some rule of thumb.
Iterative Optimization Approach
- Run 1 (Initial Solution): In the first run, you solve the route optimization problem using the initial assumption of the number of vehicles. This initial solution will likely provide a feasible but possibly suboptimal result in terms of minimizing the number of vehicles.
- Analyse and Refine: After obtaining the initial solution, you carefully analyze its performance and explore ways to improve it. You focus on the total cost of transportation, which includes factors like travel time or distance, and consider how well the customers’ demands are met while adhering to vehicle capacity constraints.
- Increment the Number of Vehicles: To refine the solution and potentially achieve better results, you increment the number of vehicles used in the next iteration. This means you consider adding more vehicles to the fleet than in the previous run.
- Run 2(Additional Vehicles): Using the increased number of vehicles, you solve the route optimization problem again. This time, the optimization algorithm can explore different vehicle assignments and paths due to the increased fleet size.
- Evaluate and Compare: Once you have the solution for the second run, you compare its performance with the initial solution. You assess factors like total transportation cost, number of vehicles used, and adherence to various constraints.
- Repeat and Converge: The iterative process continues for a few more runs, each time incrementing the number of vehicles by some value. With each iteration, the algorithm fine-tunes the vehicle assignments and paths, seeking to improve the optimization objective.
- Determining the Optimal Number of Vehicles: As the number of vehicles increases in each iteration, the total transportation cost will generally decrease. However, the improvement will start to diminish, and at some point, adding more vehicles may no longer yield significant benefits. The iterative process helps you converge to the optimal or minimum number of vehicles required to meet the customers’ demands while minimizing costs.
Benefits of Iterative Refinement
The iterative approach allows the planner to explore different fleet sizes and identify the point where adding more vehicles does not lead to substantial cost reductions. This method is particularly useful in real-world scenarios where the optimal fleet size may not be known beforehand. It also helps in adapting to changes in customer demands, traffic conditions, or operational constraints, as the route optimization can be re-run with updated data.
By the end of the iterative process, you obtain a well-optimized solution that balances efficiency, cost-effectiveness, and customer satisfaction. The approach empowers logistics managers to make data-driven decisions and allocate resources optimally, leading to improved operational performance and a more sustainable and competitive transportation system.
Initial Setup
In the initial setup section, we set some essential parameters that will be used to formulate the inputs for solving the Multi-Vehicle Routing Problem (MVRP). These parameters include:
- City Selection: The notebook enables the creation of mock data in a defined geographic area based on the chosen city. This is useful for simulating real-world scenarios and validating route optimization solutions.
- Number of Jobs: The number of random pickup/delivery jobs to be considered. This parameter allows us to explore different problem sizes and complexities, providing insights into the scalability of the route optimization algorithm.
- Starting Number of Vehicles: The initial number of vehicles considered for the first pass solution. This value serves as the starting point for the iterative process of incrementally adding vehicles in subsequent solutions.
- Vehicle Increment: The number of vehicles to add for each subsequent solution. By increasing the number of vehicles in each iteration, we can explore the impact of fleet size on the optimization results.
- Shift Start and Shift End: These parameters define the date/time of the vehicle shift’s commencement and completion. It allows us to incorporate time constraints, such as daily working hours, into the routing optimization process.
- Seating Capacity: This parameter specifies the available seating capacity in each vehicle. It is particularly relevant in scenarios where passengers are involved, such as public transportation.
By manipulating these parameters, planners can tailor the route optimization problem to their specific use cases, considering factors such as vehicle availability, customer demands, time constraints, and capacity limitations.
This notebook offers a hands-on experience, where you will interact with NextBillion.ai’s Route Optimization API to access the MVRP services, experiment with different parameter configurations, and observe how the number of vehicles affects the overall cost and efficiency of the routing solutions.
Let’s embark on this journey to discover the optimal fleet size and unveil efficient route optimization strategies to minimize the number of vehicles while delivering exceptional service to customers. Whether you are a logistics expert, a transportation planner, or a researcher exploring the world of optimization, this technical notebook will equip you with the knowledge and tools to tackle the Route Optimization Problem with finesse.
Learn how to solve route optimization problems with easy-to-follow API Tutorials.
Refer to API Documentation to learn about the optimization parameters.