Table of Contents
What is the Travelling Salesman Problem?
The Traveling Salesman Problem (TSP) is an optimization problem in which the goal is to find the shortest possible route for a given set of cities and the distances between each pair of cities while ensuring that each city is visited exactly once and returned to the starting point. In other words, it’s about finding the shortest possible tour that covers all of the cities on the list, with the constraint that the tour must begin and end in the same city, typically the home city of a traveling salesman.
The problem is frequently represented as a complete graph, with each city represented as a node and the edges between the nodes representing the distances between cities. The goal is to find the Hamiltonian cycle with the smallest total edge weight.
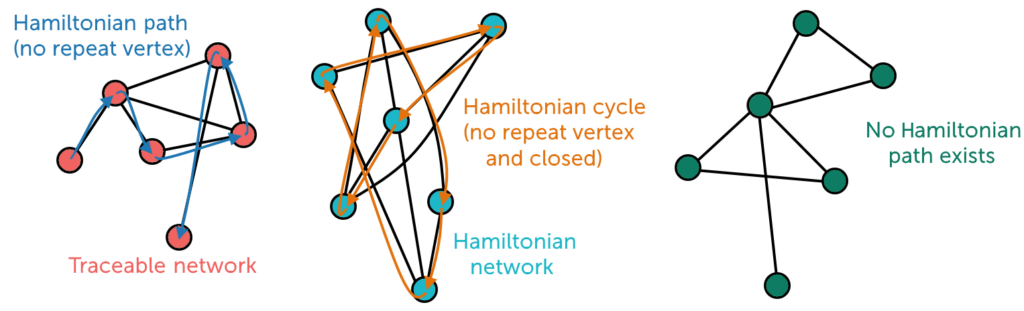
A Hamiltonian cycle, also known as a Hamiltonian circuit, is a graph theory concept. It is a type of cycle that visits each vertex (node) in a graph exactly once before returning to the beginning vertex. In other words, it is a closed path that includes every node in the graph without repetition, with the exception of the beginning and ending nodes, which are the same.
TSP is a classic example of a combinatorial optimization problem and is known to be NP-hard, which means that the problem’s complexity grows exponentially as the number of cities increases, making it computationally difficult to find an optimal solution for large instances of the problem.
TSP has applications in a variety of fields, including logistics, transportation, and manufacturing, where it is used to optimize routing and reduce travel costs. To approximate solutions to the TSP, many algorithms and heuristics have been developed, including brute force methods, dynamic programming, and various optimization techniques.
Traditional Approaches to Solve TSP
Traditionally, the TSP was solved using mathematical optimization techniques like linear programming and branch-and-bound methods. While these methods worked well for small instances, they struggled with larger datasets due to the exponential increase in computation time.
Modern Technology and TSP Solutions
The Traveling Salesman Problem (TSP) is a well-known NP-hard problem, which means that finding the optimal solution for large instances is computationally difficult. However, technology, particularly algorithms and computing power can be used to approach solutions in an efficient and effective manner. Here are some ways that technology can aid in the resolution of the TSP:
Optimization Tools
Optimization tools such as NextBillion.ai’s Route Optimization API and Route Optimization Tool leverage AI and ML algorithms and optimization techniques to solve TSP instances efficiently. These tools are useful for resolving real-world instances of the Traveling Salesman Problem. They provide efficient and practical solutions that take into account real-world constraints, handle large datasets, and adapt to changing conditions. The Route Optimization API can help businesses in a variety of industries, from logistics and transportation to field service and delivery, optimize their operations and reduce costs while increasing efficiency.
- Exact Algorithms
To solve TSP instances with a small number of cities, exact algorithms can be implemented using technology. These algorithms search through all possible combinations of cities to find the best solution. Dynamic programming and branch-and-bound algorithms are two examples. While these can handle small TSP instances, their exponential time complexity makes them unsuitable for large-scale problems.
- Heuristic Algorithms
By making educated guesses, heuristic algorithms provide practical solutions. For example, the nearest neighbor algorithm starts in one city and chooses the nearest unvisited city as the next destination. While these algorithms are not guaranteed to find the best solution, they can produce good results in a reasonable amount of time.
- Metaheuristic Algorithms
Metaheuristic algorithms, such as genetic algorithms and simulated annealing, have grown in popularity for TSP solutions. To find near-optimal solutions, these algorithms employ a combination of randomness and systematic exploration. Because of their ability to escape local optima, they are useful for larger instances.
- Machine Learning
TSP has also benefited from machine learning techniques, particularly neural networks. It is possible to find high-quality solutions by training neural networks to predict the best next city to visit. The TSP route has been gradually optimized through the use of reinforcement learning algorithms such as Q-learning.
- Parallel and Distributed Computing
Parallel computing makes use of multiple processors or machines to divide a problem into smaller subproblems that are solved concurrently. For large TSP instances, this approach significantly reduces computation time.
- Quantum Computing
The promise of quantum computing lies in its ability to solve complex problems like TSP at an exponentially faster rate. The D-Wave quantum annealers exhibit the potential for outperforming classical computers in TSP instance solving.
- Data Structures and Graph Theory
Advanced data structures and algorithms can aid in the efficient representation and manipulation of graphs in TSP instances. Techniques like graph pruning and specialized data structures can be used to reduce the time complexity of TSP algorithms.
The Traveling Salesman Problem is still a difficult and relevant problem in the fields of optimization and logistics. While its theoretical complexity is well understood, the practical application of modern technology, such as heuristic algorithms, metaheuristics, machine learning, parallel computing, and quantum computing, has paved the way for efficiently and cost-effectively solving real-world TSP instances.
As technology advances, the TSP may no longer be an insurmountable barrier. We are on the verge of solving this age-old problem with the help of innovative algorithms and computational power, reaping the benefits of optimized routes and resource allocation across multiple industries.
We know that every business is different and we care about your unique needs.
With NextBillion.ai's Map API you get- Large Distance Matrix API with a Matrix size upto than 5000*5000
- Optimal routes with accurate ETAs
- Flexible navigation SDK that's easy to integrate and ready to use for developers
- Quick and accurate location data
- Track and trace routes taken along with other map attributes
- Create custom tiles for your interactive maps. Personalized to fit your brand aesthetic.